Base numbers
There were two fundamental principles available for constructing numbersymbols: one that we might call a cardinal system, in which you adopt a standard sign for the unit and repeat it as many times as there are units in the number; and another that we could call an ordinal system, in which each number has its own distinctive symbol.
In virtue of the first principle, the numbers 2 to 4 can be represented by laying out the appropriate number of "unit signs" in pebbles, fingers, notches or dots.
The second principle gives rise to representations for the first four numbers (in words, objects or signs) that are each different from the others.
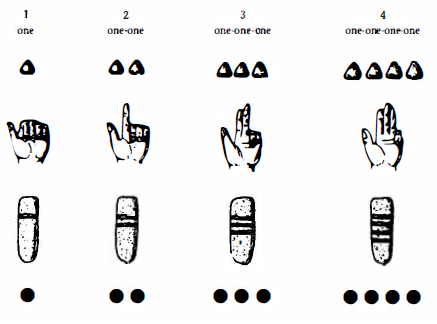
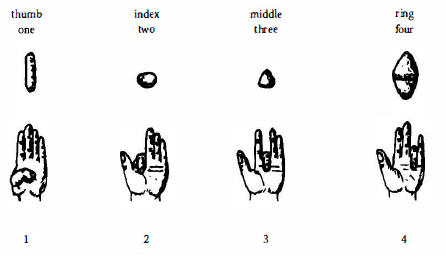
Either of these principles is an adequate basis for acquiring a grasp of ever larger sets.
To make any progress, people had first to solve a really tricky problem: What in practice is the smallest set of symbols in which the largest numbers can in theory be represented?
The solution is to give one particular set (for example, the set of ten, the set of twelve, the set of twenty or the set of sixty) a special role and to classify the regular sequence of numbers in a hierarchical relationship to the chosen ("base") set.
In other words, you agree to set up a ladder and to organise the numbers and their symbols on ascending steps of the ladder.
On the first step you call them "first-order units", on the second step, "units of the second order", on the third step, "units of the third order", and so on.
The system is called "the rule of position" (or "place-value system"), and its discovery marked the birth of numbering systems where the "base" is the number of units in the set that constitutes the unit of the next order. The place-value system can be applied to material "relays", to words in a language, or to graphic marks - producing respectively concrete, oral, and written numbering systems.


